9.9 Price-Yield Curve

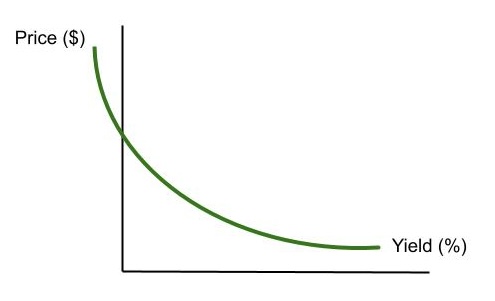If one maps out all the Prices for a given bond for the infinite set of Yields and then connects the dots, the Price/Yield Curve emerges.

Notes:

The Price – Yield Curve (PYC) is both negative (in slope) and convex (when viewed from below).

• It is negatively sloped because of TVM (i.e., the dollar-price versus yield/discount rate relationship is inverse).
• It is a curve (and not a line) because the TVM math is exponential.
• At no point does the curve go completely horizontal. The PYC is “asymptotic” to the horizontal axis, but not the vertical, with which it will intersect and continue its north-westerly movement.
  • Asymptotic means that the curve gets closer to the horizontal axis – as yields rise, but the curve never touches it, and never goes perfectly horizontal either. As a result, the curve can be described as Convex in shape when viewed from below.
  • Why asymptotic? It makes no sense that the price would be zero, i.e., at the point where the curve intercepts the horizontal axis, and the yield would be very high. At a very high yield, the price may be virtually nil, but still greater – infinitesimally so – than zero. (What if the money were worthless – like pre-WWII Reich Mark denominated Bonds?)
  • At a zero-yield, i.e., where the curve intercepts the vertical axis, the price would actually be equal to the nominal value of the bond’s aggregated cash flows, as there would be no discounting, i.e., the discount factor, (1 + R) ^N = (1 + 0) ^N = 1.
  • At a negative yield, the investor would pay more than the nominal value of the bond’s cash flows – as the curve continues to rise to the left of the vertical axis – and the investor gets back only the bond’s nominal value, i.e., (1 + R) ^N < 0.
    • A large institution may do this in a Flight to Quality, essentially paying for storing their large sums of money – usually in Treasury Bills – as a safe haven.
  • So, the PYC will intersect the vertical, but not the horizontal axis.