9.38 Negative Convexity

Bonds that have variable maturities (due to embedded options), e.g., callable bonds, mortgage-backed bonds, and sinking funds, may manifest Negative Convexity. This is a special case of (Positive) Convexity.

For example, as a callable bond may be thought of as a straight bond with an embedded call option, there are additional ramifications that need to be attended to.  If rates go up, the price of the callable bond will approximate the price of the straight bond because the call option value disappears as the likelihood of the bond’s being called evaporates.  However, if rates decline, the price of the bond will be limited by the exercise price of the call, i.e., the bond price will approximate the call price.  This is why callable bonds are normally worth less than non-callables, i.e., the non-callables are potentially more profitable and the callables thus offer a higher yield and oftentimes a higher coupon rate as well.

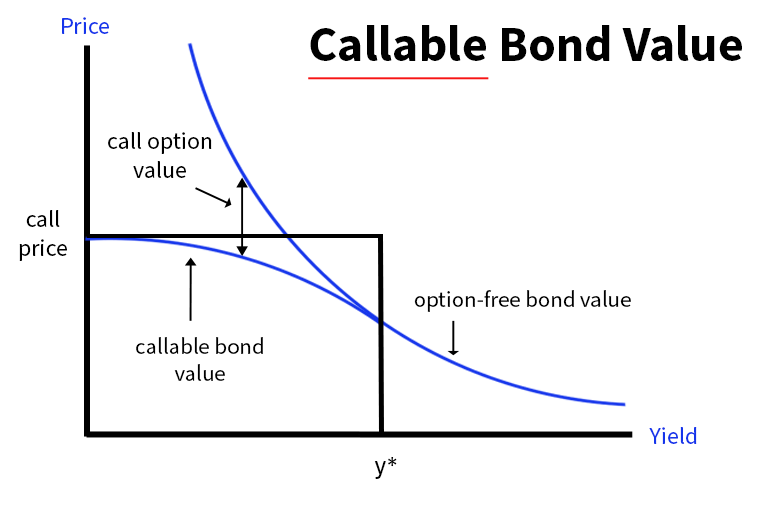Where market yields for comparable straight bonds exceed the coupon rate y*, the issuers will not call the bond and the price yield curve will be normal (i.e., positively convex – to the right of y*).  As rates decline – below y*, the likelihood of being called increases and the price/yield curve will turn negatively convex – the actual price will then be less than that predicted by the duration line.

• If as yields increase, duration decreases, the bond displays positive convexity – to the right of y*.
  • Prices decrease less with a rise in yields than if yields had fallen.
• If as yields decrease, duration will not – in this instance increase – because the bond has negative convexity – to the left of y*, i.e., the likelihood of its being called increases.
  • Prices will be capped by the “Call Penalty.”

Pricing bonds with Embedded Options

• Long Callable Bond = Long “Straight” Bond – Call Option (Issuer holds option, which is negative to the bondholder).
  • The price of a callable bond equals its price as though it were a non-callable bond less the value of the option which the issuer holds and the investor is essentially short. As the yield increases, the option value decreases to the point at which it is immaterial, hence the phrase in the diagram above “option free.”
• Long Put Bond = Long “Straight” Bond + Long Put (Put feature can cause price to rise to Par).