9.21 Price-Yield Curve: Duration

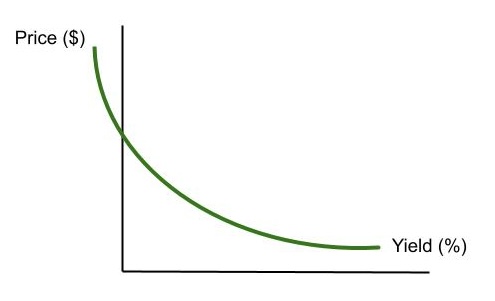
Characteristics of the P-Y Curve and Duration

1. Duration is the tangent-point of a straight line along the curve, i.e., it is the curve’s slope (∆y/∆x) at a point on the curve, which is also its first derivative. The curve’s duration/slope changes at a rate equal to its “convexity,” i.e., the second derivative.

• If you draw numerous tangent lines (i.e., duration lines) along the curve, you will note the change in slope or steepness of the lines. The P-Y curve will get steeper toward the left. Thus, for a given change in yield in either direction, price will go up more than it will go down. This represents the principle of convexity. This will be discussed in greater detail later – when we get to Convexity.

2. The Price-Yield Curve is “asymptotic” with regard to the horizontal axis, but not in reference to the vertical. Asymptotic means that the curve never touches the (horizontal) axis, but will, in infinite space, approach it, i.e., it gets forever closer and closer to it. Of course, yields can never get infinitely high. Therefore, the bond cannot have a dollar price of zero and, at the same time, a very high yield.

• The P-Y curve, however, can, first, touch the vertical axis. In this case, with the yield at zero, the bond’s price would be equal to the nominal value of its aggregated cash flows There would be no discounting of the cash flows at a zero percent discount rate. “(1+R)ⁿ” will always equal one so none of the bond’s cash flows would be discounted and the bond’s price would simply equal the nominal sum of its cash flows.

• Moreover, if yields turn negative, the P-Y Curve would resume its upward climb to the left side of the vertical axis, intersecting it and continuing. This would mean that the price one paid for the bond would exceed the aggregated, nominal value of the bond’s cash flows. If R < 0, each cash flow’s divisor –  “(1+R)ⁿ” – would be less than one; dividing by a number, which is less than one would get an outcome greater than the numerator. The investor would thus be paying the issuer merely to hold the bond for the investor, i.e., a kind of “storage cost.” And would receive back less than the nominal value of the bond’s cash flows. S/he’d lose money, in short.

• We have seen rates, for a brief time (during the banking crisis of 2007-2008) dip into negative territory, and in 2020, rates were negative in Japan and in parts of Europe. In a “flight to quality,” American investors fear owning risky securities and invest instead in safe-haven, Treasuries. During a flight to quality, Treasury yields can go negative, but could Corporates? It is unlikely that anyone would buy Corporates when they could buy, presumably more secure, Treasuries instead.